To perform analyses on WASM programs, it is possible to build a CFG of the function bodies.
Computation
A CFG is computed using a Traverser, for instance to compute CFGs for the naive fibonacci function, you can do this way
import swam.text._
import swam.cfg._
import cats.effect._
import java.nio.file.Paths
implicit val cs = IO.contextShift(scala.concurrent.ExecutionContext.global)
val cfg =
Blocker[IO].use { blocker =>
for {
compiler <- Compiler[IO](blocker)
naive <- compiler.compile(Paths.get("fibo.wat"), blocker).map(_.funcs(0))
cfg <- CFGicator.buildCFG[IO](naive.body)
} yield cfg
}.unsafeRunSync()
The CFG can be traversed in postorder (depth first) using the CFG.postorder function, that makes it possible to compute a value by accumulation.
For instance, to build the list of nodes in reverse postorder, one can do:
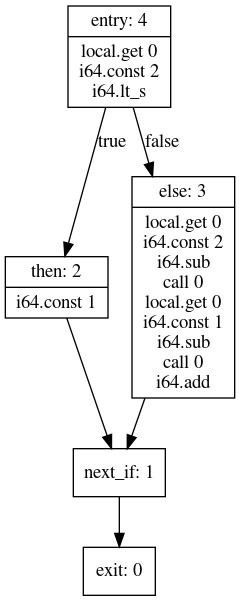
val reversePostorder = cfg.postorder(List.empty[BasicBlock])((acc, block) => block :: acc)
// reversePostorder: List[BasicBlock] = List(
// BasicBlock(4, "entry", List(LocalGet(0), Const(2L), LtS), Some(If(2, 3))),
// BasicBlock(
// 3,
// "else",
// List(
// LocalGet(0),
// Const(2L),
// Sub,
// Call(0),
// LocalGet(0),
// Const(1L),
// Sub,
// Call(0),
// Add
// ),
// Some(To(1))
// ),
// BasicBlock(2, "then", List(Const(1L)), Some(To(1))),
// BasicBlock(1, "next_if", List(), Some(To(0))),
// BasicBlock(0, "exit", List(), None)
// )
This is a common ordering when working with CFG, and is available through the CFG.reversePostorder method.
Pretty Printing
For debugging or documentation purpose, it might be handy to pretty-print the CFGs.
Swam provides a Show instance that prints the CFG to a dot graph.
import swam.cfg.dot._
import cats.implicits._
println(cfg.show)
// digraph {
// rankdir=TB;
// node[shape=record];
// bb0[label="exit: 0"];
// bb1[label="next_if: 1"];
// bb1->bb0;
// bb2[label="{then: 2|i64.const 1}"];
// bb2->bb1;
// bb3[label="{else: 3|local.get 0\ni64.const 2\ni64.sub\ncall 0\nlocal.get 0\ni64.const 1\ni64.sub\ncall 0\ni64.add}"];
// bb3->bb1;
// bb4[label="{entry: 4|local.get 0\ni64.const 2\ni64.lt_s}"];
// bb4->bb2[label="true"];
// bb4->bb3[label="false"]
// }
The generated code can be compiled to get an image of it. In this example, it renders as: